黑题记录-2D Geometry 110 in 1!

题目链接：https://www.luogu.com.cn/problem/UVA12304

题面翻译

欢迎来到二维计算几何问题合一~！

你需要写一个程序，回答以下的询问。

请仔细阅读输入输出格式！

询问：求外接圆

输入格式：CircumscribedCircle
输出格式：(x,y,r)，其中描述圆心的位置，表示圆的半径。
描述：给定三角形，顶点分别为，，，求出这个三角形的外接圆的圆心和半径。
约定：保证三点不共线。

询问：求内切圆

输入格式：InscribedCircle
输出格式：(x,y,r)，其中描述圆心的位置，表示圆的半径。
描述：给定三角形，顶点分别为，，，求出这个三角形的内切圆的圆心和半径。
约定：保证三点不共线。

询问：过一点求切线

输入格式：TangentLineThroughPoint
输出格式：[angle1,angle2]
- 输出一个列表（类似 Python 中的数组），列表中含有几个（或者个）实数，以角度描述切线的倾斜角。注意单位是角度，你需要保证。
- 你需要保证列表中的元素是升序排列的。
- 若无解，输出空列表 []。
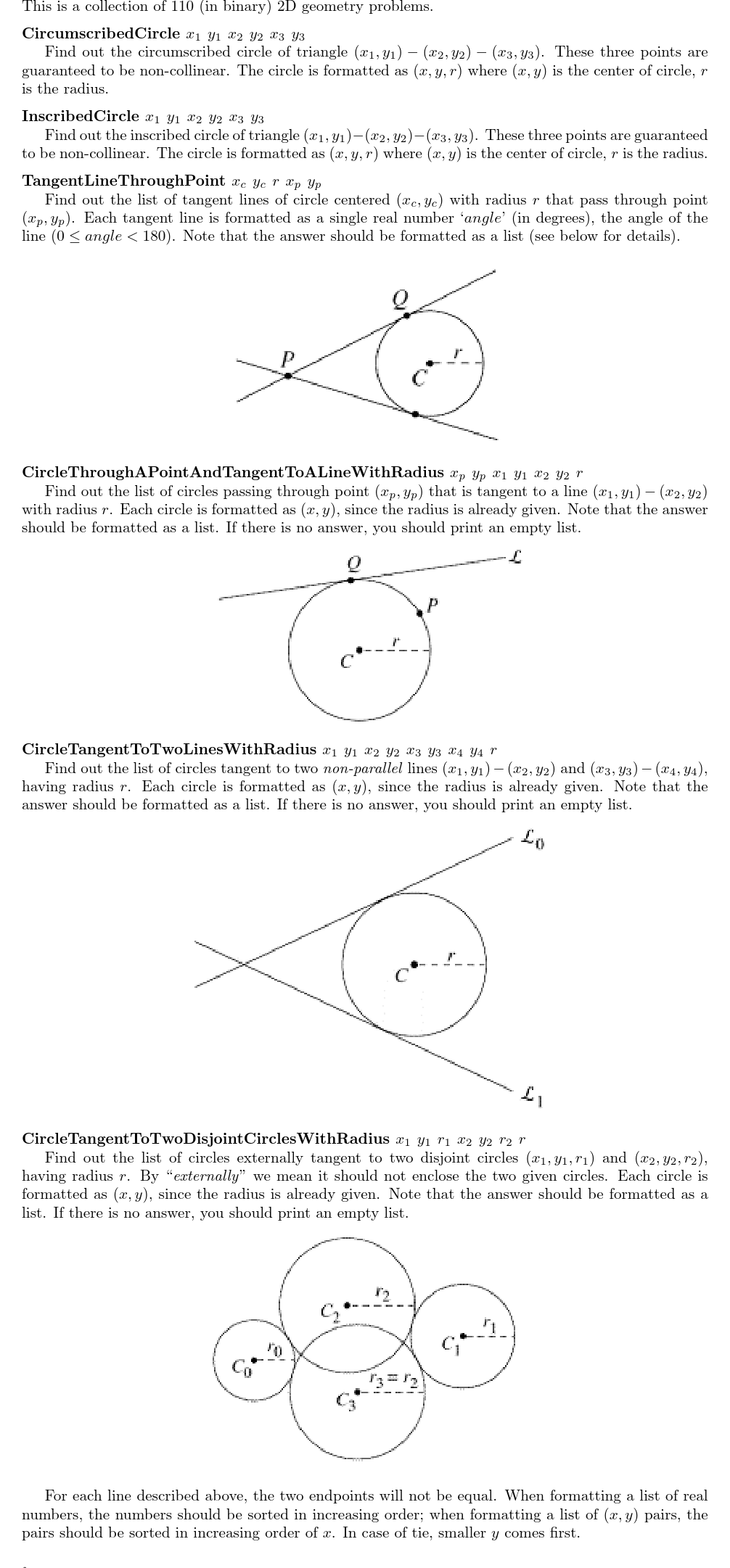
描述：给定一个以为圆心，为半径的圆和一个点，求出过且与圆相切的所有直线。

询问：求与一条已知直线相切、过已知点且固定半径的圆

输入格式：CircleThroughAPointAndTangentToALineWithRadius =
输出格式：[(x1,y1),(x2,y2)]
- 输出一个列表（类似 Python 中的数组），列表中含有几个（或者个）二元组，描述一个圆的圆心。
- 你需要保证列表中的元素以为第一关键字，为第二关键字升序排列。
- 若无解，输出空列表 []。
描述：给定过和的直线，点和半径。你需要求出所有的圆，满足以下条件：
- 与相切。
- 点在圆上。
- 的半径为。

询问：求与两条已知直线相切且固定半径的圆

输入格式：CircleTangentToTwoLinesWithRadius
输出格式：[(x1,y1),(x2,y2)]
- 同询问中的输出。
- 输出一个列表（类似 Python 中的数组），列表中含有几个（或者个）二元组，描述一个圆的圆心。
- 你需要保证列表中的元素以为第一关键字，为第二关键字升序排列。
- 若无解，输出空列表 []。
描述：给定过和的直线，过和的直线和半径。你需要求出所有的圆，满足以下条件：
- 与和都相切。
- 的半径为。
约定：保证不与平行。

询问：求固定半径的公共外切圆

输入格式：CircleTangentToTwoDisjointCirclesWithRadius
输出格式：[(x1,y1),(x2,y2)]
- 同询问中的输出。
- 输出一个列表（类似 Python 中的数组），列表中含有几个（或者个）二元组，描述一个圆的圆心。
- 你需要保证列表中的元素以为第一关键字，为第二关键字升序排列。
- 若无解，输出空列表 []。
描述：给定圆，半径为，圆心坐标为和圆，半径为，圆心坐标为。且给定。你需要求出所有的圆，满足以下条件：
- 与和外切。也就是说，不能把或者包含在（）内。
- 的半径为。

请注意：

输出时，对于列表元素是实数的情况，你需要保证列表中的元素是升序的。
输出时，对于列表元素是二元组的情况，你需要保证这些二元组以为第一关键字，为第二关键字升序排列。
无解的时候输出空列表 []。
你的输出中不应包含空格。
每个输出的数字保留位小数。

输入格式

本题有多组数据。数据组数不超过。

对于每行，有一个询问，格式如上所述。保证所有输入的数字均为整数，且绝对值不大于。

数据以 EOF（文件终止符）结尾。

输出格式

对于每个询问，输出结果，格式如上所述。

每个输出的数字应保留位小数。

对于每个列表，以中括号 [] 包裹；对于每个二元组，以小括号 () 包裹。你的输出中不应包含空格。

题目描述

PDF

输入格式

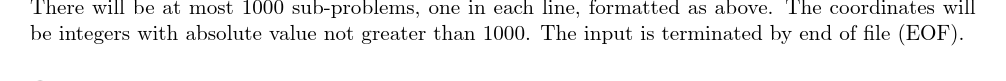
输出格式

样例 #1

样例输入 #1

CircumscribedCircle 0 0 20 1 8 17
InscribedCircle 0 0 20 1 8 17
TangentLineThroughPoint 200 200 100 40 150
TangentLineThroughPoint 200 200 100 200 100
TangentLineThroughPoint 200 200 100 270 210
CircleThroughAPointAndTangentToALineWithRadius 100 200 75 190 185 65 100
CircleThroughAPointAndTangentToALineWithRadius 75 190 75 190 185 65 100
CircleThroughAPointAndTangentToALineWithRadius 100 300 100 100 200 100 100
CircleThroughAPointAndTangentToALineWithRadius 100 300 100 100 200 100 99
CircleTangentToTwoLinesWithRadius 50 80 320 190 85 190 125 40 30
CircleTangentToTwoDisjointCirclesWithRadius 120 200 50 210 150 30 25
CircleTangentToTwoDisjointCirclesWithRadius 100 100 80 300 250 70 50

样例输出 #1

(9.734940,5.801205,11.332389)
(9.113006,6.107686,5.644984)
[53.977231,160.730818]
[0.000000]
[]
[(112.047575,299.271627),(199.997744,199.328253)]
[(-0.071352,123.937211),(150.071352,256.062789)]
[(100.000000,200.000000)]
[]
[(72.231286,121.451368),(87.815122,63.011983),(128.242785,144.270867),(143.826621,85.831483)]
[(157.131525,134.836744),(194.943947,202.899105)]
[(204.000000,178.000000)]

AC代码

#include <ostream>
#include <utility>
#include <bits/stdc++.h>

using namespace std;

using ll = long long;
using ld = long double;

static const auto _ = []() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    return nullptr;
}();

constexpr ld eps = 1e-6;

inline int checkZero(const double x) {
    if (-eps <= x && x <= eps) return 0;
    return x > 0 ? 1 : -1;
}

struct Point {
    ld x, y;

    Point() = default;

    Point(const ld x, const ld y): x(x), y(y) {
    }

    ~Point() = default;

    Point(const Point& other) = default;

    Point(Point&& other) noexcept: x(other.x), y(other.y) {
    }

    Point& operator=(const Point& other) {
        if (this == &other)
            return *this;
        x = other.x;
        y = other.y;
        return *this;
    }

    Point& operator=(Point&& other) noexcept {
        if (this == &other)
            return *this;
        x = other.x;
        y = other.y;
        return *this;
    }

    friend istream& operator>>(istream& in, Point& o) {
        return in >> o.x >> o.y;
    }

    friend bool operator<(const Point& lhs, const Point& rhs) {
        return lhs.x == rhs.x ? lhs.y < rhs.y : lhs.x < rhs.x;
    }

    Point operator+(const Point& t) const { return {x + t.x, y + t.y}; }
    Point operator-(const Point& t) const { return {x - t.x, y - t.y}; }
    Point operator-() const { return {-x, -y}; }
    Point operator*(const ld t) const { return {x * t, y * t}; } //数乘
    void operator*=(const ld t) { x *= t, y *= t; } //数乘
    Point operator/(const ld t) const { return checkZero(t) == 0 ? Point() : Point{x / t, y / t}; }
    void operator/=(const ld t) { x /= t, y /= t; }
    ld norm() const { return sqrt(x * x + y * y); }
    Point rotate() { return *this = {y, -x}; }
};

using Vec = Point;

struct Line {
    Point s;
    Vec v;

    Line() = default;

    Line(Point s, Vec v): s(std::move(s)), v(std::move(v)) {
    }

    Line(const Line& other) = default;

    ~Line() = default;

    Line(Line&& other) noexcept : s(std::move(other.s)), v(std::move(other.v)) {
    }

    Line& operator=(const Line& other) {
        if (this == &other)
            return *this;
        s = other.s;
        v = other.v;
        return *this;
    }

    Line& operator=(Line&& other) noexcept {
        if (this == &other)
            return *this;
        s = std::move(other.s);
        v = std::move(other.v);
        return *this;
    }
};

inline ld cross(const Point& a, const Point& b) { return a.x * b.y - a.y * b.x; } //叉积
inline ld dot(const Point& a, const Point& b) { return a.x * b.x + a.y * b.y; } //点积

inline ld dis(const Point& a, const Point& b) { return sqrt(dot(a - b, a - b)); } //距离
inline ld dis(const Point& p, const Line& l) {
    const Vec a = p - l.s;
    const ld d = dot(a, l.v) / l.v.norm();
    return sqrt(pow(a.norm(), 2) - d * d);
}

inline Point inter(const Line& l1, const Line& l2) {
    const Point t1 = l1.s + l1.v;
    const ld s1 = cross(l2.v, l1.s - l2.s);
    const ld s2 = cross(t1 - l2.s, l2.v);
    const ld t = s1 / (s1 + s2);
    return l1.s + l1.v * t;
}

inline string streamput(vector<Point>& v) {
    stringstream ss;
    ss << fixed << setprecision(6);
    for (const auto& l: v)
        ss << '(' << l.x << ',' << l.y << ')' << ',';
    string s = ss.str();
    s.pop_back();
    return s;
}

inline double CheckAngleAndChange(double angle) {
    // Change to [0, 180)
    if (checkZero(angle) == -1)
        while (checkZero(angle) == -1) angle += 180.0;
    else if (checkZero(angle - 180.0) != -1)
        while (checkZero(angle - 180.0) != -1) angle -= 180.0;
    return angle;
}

inline void CircumscribedCircle() {
    Point p1, p2, p3;
    cin >> p1 >> p2 >> p3;
    const Line l12((p1 + p2) / 2.0, (p1 - p2).rotate());
    const Line l13((p1 + p3) / 2.0, (p1 - p3).rotate());
    const Point o = inter(l12, l13);
    const ld r = dis(o, p1);
    cout << '(' << o.x << ',' << o.y << ',' << r << ')' << '\n';
}

inline void InscribedCircle() {
    Point p1, p2, p3;
    cin >> p1 >> p2 >> p3;
    const Line c12(p3, (p1 - p3) / dis(p1, p3) + (p2 - p3) / dis(p2, p3));
    const Line c13(p2, (p1 - p2) / dis(p1, p2) + (p3 - p2) / dis(p3, p2));
    const Point o = inter(c12, c13);
    const ld r = dis(o, Line{p1, p2 - p1});
    cout << '(' << o.x << ',' << o.y << ',' << r << ')' << '\n';
}

inline void TangentLineThroughPoint() {
    Point p, o;
    ld r;
    cin >> o >> r >> p;
    const ld d = dis(o, p);
    if (d < r) {
        cout << "[]\n";
        return;
    }
    if (fabs(d - r) < eps) {
        auto [x, y] = (p - o).rotate();
        ld ans = atan2(y, x);
        ans *= 180 / M_PI;
        ans = CheckAngleAndChange(ans);
        cout << '[' << ans << ']' << '\n';
    } else {
        const Vec pv = p - o;
        const ld cha = asin(r / pv.norm());
        const ld ac = atan2(pv.y, pv.x);
        vector<ld> ans(2);
        ans[0] = (ac + cha) * 180 / M_PI;
        ans[1] = (ac - cha) * 180 / M_PI;
        for (ld& a: ans) a = CheckAngleAndChange(a);
        ranges::sort(ans);
        cout << '[' << ans[0] << ',' << ans[1] << ']' << '\n';
    }
}

inline void CircleThroughAPointAndTangentToALineWithRadius() {
    Point p, a, b;
    ld r;
    cin >> p >> a >> b >> r;
    const Line ab(a, b - a);
    const ld d = dis(p, ab);
    if (d - r * 2.0 > eps) {
        cout << "[]\n";
        return;
    }
    Vec c = ab.v;
    c.rotate();
    c /= c.norm();
    c *= r;
    vector<pair<Line, ld>> lines = {{Line(ab.s + c, ab.v), 0}, {Line(ab.s - c, ab.v), 0}};
    lines[0].second = dis(p, lines[0].first);
    lines[1].second = dis(p, lines[1].first);
    if (lines[1].second - r > eps) lines.erase(lines.begin() + 1, lines.end());
    if (lines[0].second - r > eps) lines.erase(lines.begin(), lines.begin() + 1);
    vector<Point> ans;
    for (auto& [l,dist]: lines) {
        const ld k = sqrt(fabs(r * r - dist * dist));
        Vec tmp = l.v;
        Point pa = inter(l, Line(p, tmp.rotate()));
        if (k < eps) {
            ans.push_back(pa);
            continue;
        }
        Vec vp = l.v / l.v.norm() * k;
        ans.push_back(pa + vp);
        ans.push_back(pa - vp);
    }
    sort(ans.begin(), ans.end());
    cout << '[' << streamput(ans) << ']' << '\n';
}

inline void CircleTangentToTwoLinesWithRadius() {
    Line a, b;
    ld r;
    cin >> a.s >> a.v >> b.s >> b.v >> r;
    a.v = a.v - a.s, b.v = b.v - b.s;
    Vec ta = a.v / a.v.norm(), tb = b.v / b.v.norm();
    ta.rotate(), tb.rotate();
    ta *= r, tb *= r;
    vector<Point> ans;
    ans.reserve(4);
    ans.push_back(inter({a.s + ta, a.v}, {b.s + tb, b.v}));
    ans.push_back(inter({a.s + ta, a.v}, {b.s - tb, b.v}));
    ans.push_back(inter({a.s - ta, a.v}, {b.s + tb, b.v}));
    ans.push_back(inter({a.s - ta, a.v}, {b.s - tb, b.v}));
    sort(ans.begin(), ans.end());
    cout << '[' << streamput(ans) << ']' << '\n';
}

inline void CircleTangentToTwoDisjointCirclesWithRadius() {
    Point a, b;
    ld r1, r2, r;
    cin >> a >> r1 >> b >> r2 >> r;
    ld d = dis(a, b);
    r1 += r, r2 += r;
    if (d - (r1 + r2) >= eps || fabs(r2 - r1) - d >= eps) {
        cout << "[]\n";
        return;
    }
    if (fabs(d - (r1 + r2)) < eps || d - fabs(r2 - r1) < eps) {
        const Vec v = (b - a) / d * r1;
        Point o = a + v;
        cout << "[(" << o.x << ',' << o.y << ")]" << '\n';
        return;
    }
    ld ap = (pow(r1, 2) + pow(d, 2) - pow(r2, 2)) / (2 * d);
    Point p = a + (b - a) / d * ap;
    ld k = sqrt(r1 * r1 - ap * ap);
    Vec v = (b - a).rotate() / d * k;
    vector<Point> ans = {p + v, p - v};
    sort(ans.begin(), ans.end());
    cout << '[' << streamput(ans) << ']' << '\n';
}

int main() {
    // DEBUG
    // freopen("../in.txt", "r", stdin);
    string s;
    unordered_map<string, char> m{
        {"CircumscribedCircle", 1},
        {"InscribedCircle", 2},
        {"TangentLineThroughPoint", 3},
        {"CircleThroughAPointAndTangentToALineWithRadius", 4},
        {"CircleTangentToTwoLinesWithRadius", 5},
        {"CircleTangentToTwoDisjointCirclesWithRadius", 6}
    };
    cout << fixed << setprecision(6);
    while (cin >> s) {
        switch (m[s]) {
            case 1: CircumscribedCircle();
                break;
            case 2: InscribedCircle();
                break;
            case 3: TangentLineThroughPoint();
                break;
            case 4: CircleThroughAPointAndTangentToALineWithRadius();
                break;
            case 5: CircleTangentToTwoLinesWithRadius();
                break;
            case 6: CircleTangentToTwoDisjointCirclesWithRadius();
        }
    }
    return 0;
}

题面翻译

询问：求外接圆

询问：求内切圆

询问：过一点求切线

询问：求与一条已知直线相切、过已知点且固定半径的圆

询问：求与两条已知直线相切且固定半径的圆

询问：求固定半径的公共外切圆

输入格式

输出格式

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

AC代码

常用STL算法库汇总

dinic算法和LuoGu P1343 地震逃生

stazxr

题面翻译

询问 ：求外接圆

询问 ：求内切圆

询问 ：过一点求切线

询问 ：求与一条已知直线相切、过已知点且固定半径的圆

询问 ：求与两条已知直线相切且固定半径的圆

询问 ：求固定半径的公共外切圆

输入格式

输出格式

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

AC代码

常用STL算法库汇总

dinic算法和LuoGu P1343 地震逃生

stazxr

询问：求外接圆

询问：求内切圆

询问：过一点求切线

询问：求与一条已知直线相切、过已知点且固定半径的圆

询问：求与两条已知直线相切且固定半径的圆

询问：求固定半径的公共外切圆