P3517 [POI2011] WYK-Plot

题目描述

We call any sequence of points in the plane a plot.

We intend to replace a given plot with another that will have at most points () in such a way that it “resembles” the original plot best.

The new plot is created as follows. The sequence of points can be partitioned into () contiguous subsequences:

where ,and afterwards each subsequence , for ,is replaced by a new point .

In that case we say that each of the points has been contracted to the point .

As a result a new plot, represented by the points , is created.

The measure of such plot’s resemblance to the original is the maximum distance of all the points to the point it has been contracted to:

where denotes the distance between and , given by the well-known formula:

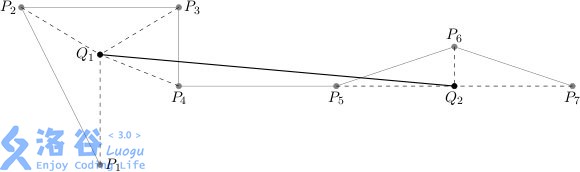
An exemplary plot and the new plot , where are contracted to , whereas to .

For a given plot consisting of points, you are to find the plot that resembles it most while having at most points, where the partitioning into contiguous subsequences is arbitrary.

Due to limited precision of floating point operations, a result is deemed correct if its resemblance to the given plot is larger than the optimum resemblance by at most .

给定n个点，要求把n个点分成不多于m段，使得求出每段的最小覆盖圆的半径后，最大的半径最小。

输入格式

In the first line of the standard input there are two integers and , , separated by a single space.

Each of the following lines holds two integers, separated by a single space.

The -th line gives ,, denoting the coordinates of the point .

输出格式

In the first line of the standard output one real number should be printed out, the resemblance measure of the plot found to the original one.

In the second line of the standard output there should be another integer , .

Next, the following lines should specify the coordinates of the points ,one point per line.

Thus the -th line should give two real numbers and , separated by a single space, that denote the coordinates of the point .All the real numbers should be printed with at most 15 digits after the decimal point.

样例 #1

样例输入 #1

样例输出 #1

3.00000000
2
2.00000000 1.76393202
11.00000000 1.99998199

提示

给定n个点，要求把n个点分成不多于m段，使得求出每段的最小覆盖圆的半径后，最大的半径最小。

题目大意

1.题意：给一个有个元素的点集，要求把n个点划分成不多于m个子集，使得求出每点集的最小覆盖圆的半径后，使得最大的半径最小。

解题思路

采取二分答案的思路，对圆半径进行二分答案，然后对于每个圆半径，我们可以采取随机增量法，随机增量法是一种求解最小圆覆盖的方法，其思路是随机选取一个点，然后遍历所有点，如果有点不在圆内，那么就更新圆心，然后再次遍历所有点，如果有点不在圆内，那么就更新圆心和半径，然后再次遍历所有点，如果有点不在圆内，那么就更新圆心和半径，这样就可以求出最小圆覆盖的圆心和半径。

不会随机增量法的先去做最小圆覆盖

check 函数用于判断是否可以将所有点分成不多于 m 个子集，使得求出每个子集的最小覆盖圆的半径后，最大的半径不超过 lim。

check 函数内部，同样使用二分答案，对于每个子集，使用随机增量法求出最小圆覆盖的圆心和半径，然后判断是否满足条件。

bool check(ld lim) {
    cnt = 0;
    int ans;
    for (int i = 1; i <= n; i = ans + 1) {
        int k;
        for (k = 1; i + (1 << k) - 1 <= n; ++k) {
            random_increment(i, i + (1 << k) - 1);
            if (d > lim + eps) break;
        }
        ans = i;
        int l = i + (1 << (k - 1)) - 1, r = min(n, i + (1 << k) - 1);
        while (l <= r) {
            int mid = (l + r) >> 1;
            random_increment(i, mid);
            if (d < lim + eps) l = mid + 1, ans = mid;
            else r = mid - 1;
        }
        ++cnt;
        res[cnt][0] = i, res[cnt][1] = ans;
        if (cnt > m) return false;
    }
    return true;
}

代码

#include <iostream>
#include <algorithm>
#include <cmath>
#include <random>
#include <iomanip>

using namespace std;

using ld = long double;

struct node {
    ld x, y;

    inline ld length() const {
        return fabs(pow(x, 2) + pow(y, 2));
    }

    inline void transfer() {
        x = -x;
        swap(x, y);
    }

    node operator/(ld v) const { return node{x / v, y / v}; }

    node operator*(ld v) const { return node{x * v, y * v}; }

    friend node operator+(node &n1, node &n2) { return node{n1.x + n2.x, n1.y + n2.y}; }

    friend node operator+(node &n1, node &&n2) { return node{n1.x + n2.x, n1.y + n2.y}; }

    friend node operator-(node &n1, node &n2) { return node{n1.x - n2.x, n1.y - n2.y}; }

    friend node operator*(node &n1, node &n2) { return node{n1.x * n2.x, n1.y * n2.y}; }
};

inline ld dis(node &p1, node &p2) {
    return sqrt((p1 - p2).length());
}

inline ld cross(const node &p1, node &p2) {
    return (p1.x * p2.y) - (p1.y * p2.x);
}

inline node get_circle(node &p1, node &p2) {
    return (p1 + p2) / 2.0;
}

inline node get_circle(node &p1, node &p2, node &p3) {
    node v1 = p2 - p1, v2 = p3 - p1;
    v1.transfer(), v2.transfer();
    node m1 = (p1 + p2) / 2.0, m2 = (p1 + p3) / 2.0;
    ld t = cross(m2 - m1, v2) / cross(v1, v2);
    return m1 + (v1 * t);
}

const ld eps = 1e-10;
const int N = 1e5 + 5;
int n, m, cnt;
int res[N][2];
node v[N], ps[N];
node o{};
ld d;
random_device rd;
mt19937 g(rd());

// 随机增量
inline void random_increment(int l, int r) {
    copy(ps + l, ps + r + 1, v);
    int len = r + 1 - l;
    shuffle(v, v + len, g);
    o = v[0], d = 0;
    for (int i = 0; i < len; ++i) {
        if (dis(o, v[i]) > d + eps) {
            o = v[i], d = 0;
            for (int j = 0; j < i; ++j) {
                if (dis(o, v[j]) > d + eps) {
                    o = get_circle(v[i], v[j]);
                    d = dis(o, v[j]);
                    for (int k = 0; k < j; ++k) {
                        if (dis(o, v[k]) > d + eps) {
                            o = get_circle(v[i], v[j], v[k]);
                            d = dis(o, v[i]);
                        }
                    }
                }
            }
        }
    }
}

bool check(ld lim) {
    cnt = 0;
    int ans;
    for (int i = 1; i <= n; i = ans + 1) {
        int k;
        for (k = 1; i + (1 << k) - 1 <= n; ++k) {
            random_increment(i, i + (1 << k) - 1);
            if (d > lim + eps) break;
        }
        ans = i;
        int l = i + (1 << (k - 1)) - 1, r = min(n, i + (1 << k) - 1);
        while (l <= r) {
            int mid = (l + r) >> 1;
            random_increment(i, mid);
            if (d < lim + eps) l = mid + 1, ans = mid;
            else r = mid - 1;
        }
        ++cnt;
        res[cnt][0] = i, res[cnt][1] = ans;
        if (cnt > m) return false;
    }
    return true;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) {
        cin >> ps[i].x >> ps[i].y;
    }
    random_increment(1, n);
    ld l = 0, r = d;
    if (m > 1) {
        while (r - l > eps) {
            ld mid = (l + r) / 2.0;
            if (check(mid)) r = mid;
            else l = mid;
        }
    }
    check(r);
    cout << fixed << setprecision(8);
    cout << r << '\n' << cnt << '\n';
    for (int i = 1; i <= cnt; ++i) {
        random_increment(res[i][0], res[i][1]);
        cout << o.x << ' ' << o.y << '\n';
    }
    return 0;
}

复杂度分析

时间复杂度：

P3517 [POI2011] WYK-Plot